Средний уровень

Прямоугольный треугольник. Полный иллюстрированный гид (2019)

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. НАЧАЛЬНЫЙ УРОВЕНЬ.

В задачах прямой угол вовсе не обязательно - левый нижний, так что тебе нужно научиться узнавать прямоугольный треугольник и в таком виде,

и в таком,

и в таком

Что же хорошего есть в прямоугольном треугольнике? Ну..., во-первых, есть специальные красивые названия для его сторон.

Внимание на рисунок!

Запомни и не путай: катетов - два, а гипотенуза - всего одна (единственная, неповторимая и самая длинная)!

Ну вот, названия обсудили, теперь самое важное: Теорема Пифагора.

Теорема Пифагора.

Эта теорема - ключик к решению многих задачек с участием прямоугольного треугольника. Её доказал Пифагор в совершенно незапамятные времена, и с тех пор она принесла много пользы знающим её. А самое хорошее в ней то, что она - простая.

Итак, Теорема Пифагора:

Помнишь шутку: «Пифагоровы штаны на все стороны равны!»?

Давай нарисуем эти самые пифагоровы штаны и посмотрим на них.

Правда, похоже на какие - то шорты? Ну и на какие стороны и где она равны? Почему и откуда возникла шутка? А шутка эта связана как раз с теоремой Пифагора, точнее с тем, как сам Пифагор формулировал свою теорему. А формулировал он её так:

«Сумма площадей квадратов , построенных на катетах, равна площади квадрата , построенного на гипотенузе».

Правда, немножко по-другому звучит? И вот, когда Пифагор нарисовал утверждение своей теоремы, как раз и получилась такая картинка.

На этой картинке сумма площадей маленьких квадратов равна площади большого квадрата. А чтобы дети лучше запоминали, что сумма квадратов катетов равна квадрату гипотенузы, кто-то остроумный и выдумал эту шутку про Пифагоровы штаны.

Почему же мы сейчас формулируем теорему Пифагора

А Пифагор мучился и рассуждал про площади?

Понимаешь, в древние времена не было… алгебры! Не было никаких обозначений и так далее. Не было надписей. Представляешь, как бедным древним ученикам было ужасно запоминать всё словами??! А мы можем радоваться, что у нас есть простая формулировка теоремы Пифагора. Давай её ещё раз повторим, чтобы лучше запомнить:

Теперь уже должно быть легко:

Ну вот, самую главную теорему о прямоугольном треугольнике обсудили. Если тебе интересно, как она доказывается, читай следующие уровни теории, а сейчас пойдём дальше… в тёмный лес… тригонометрии! К ужасным словам синус, косинус, тангенс и котангенс.

Синус, косинус, тангенс, котангенс в прямоугольном треугольнике.

На самом деле все совсем не так страшно. Конечно, «настоящее» определение синуса, косинуса, тангенса и котангенса нужно смотреть в статье . Но очень не хочется, правда? Можем обрадовать: для решения задач про прямоугольный треугольник можно просто заполнить следующие простые вещи:

А почему же всё только про угол? Где же угол? Для того, чтобы в этом разобраться, нужно знать, как утверждения 1 - 4 записываются словами. Смотри, понимай и запоминай!

1.
Вообще-то звучит это так:

А что же угол? Есть ли катет, который находится напротив угла, то есть противолежащий (для угла) катет? Конечно, есть! Это катет!

А как же угол? Посмотри внимательно. Какой катет прилегает к углу? Конечно же, катет. Значит, для угла катет - прилежащий, и

А теперь, внимание! Посмотри, что у нас получилось:

Видишь, как здорово:

Теперь перейдём к тангенсу и котангенсу.

Как это теперь записать словами? Катет каким является по отношению к углу? Противолежащим, конечно - он «лежит» напротив угла. А катет? Прилегает к углу. Значит, что у нас получилось?

Видишь, числитель и знаменатель поменялись местами?

И теперь снова углы и совершили обмен:

Резюме

Давай вкратце запишем всё, что мы узнали.

Теорема Пифагора:

Главная теорема о прямоугольном треугольнике - теорема Пифагора.

Теорема Пифагора

Кстати, хорошо ли ты помнишь, что такое катеты и гипотенуза? Если не очень, то смотри на рисунок - освежай знания

Вполне возможно, что ты уже много раз использовал теорему Пифагора, а вот задумывался ли ты, почему же верна такая теорема. Как бы её доказать? А давай поступим, как древние греки. Нарисуем квадрат со стороной.

Видишь, как хитро мы поделили его стороны на отрезки длин и!

А теперь соединим отмеченные точки

Тут мы, правда ещё кое что отметили, но ты сам посмотри на рисунок и подумай, почему так.

Чему же равна площадь большего квадрата? Правильно, . А площадь меньшего? Конечно, . Осталась суммарная площадь четырех уголков. Представь, что мы взяли их по два и прислонили друг к другу гипотенузами. Что получилось? Два прямоугольника. Значит, площадь «обрезков» равна.

Давай теперь соберем всё вместе.

Преобразуем:

Вот и побывали мы Пифагором - доказали его теорему древним способом.

Прямоугольный треугольник и тригонометрия

Для прямоугольного треугольника выполняются следующие соотношения:

Синус острого угла равен отношению противолежащего катета к гипотенузе

Косинус острого угла равен отношению прилежащего катета к гипотенузе.

Тангенс острого угла равен отношению противолежащего катета к прилежащему катету.

Котангенс острого угла равен отношению прилежащего катета к противолежащему катету.

И ещё раз всё это в виде таблички:

Это очень удобно!

Признаки равенства прямоугольных треугольников

I. По двум катетам

II. По катету и гипотенузе

III. По гипотенузе и острому углу

IV. По катету и острому углу

a)

b)

Внимание! Здесь очень важно, чтобы катеты были «соответствующие». Например, если будет так:

То ТРЕУГОЛЬНИКИ НЕ РАВНЫ , несмотря на то, что имеют по одному одинаковому острому углу.

Нужно, чтобы в обоих треугольниках катет был прилежащим, или в обоих - противолежащим .

Ты заметил, чем отличаются признаки равенства прямоугольных треугольников от обычных признаков равенства треугольников? Загляни в тему « и обрати внимание на то, что для равенства «рядовых» треугольников нужно равенство трех их элементов: две стороны и угол между ними, два угла и сторона между ними или три стороны. А вот для равенства прямоугольных треугольников достаточно всего двух соответственных элементов. Здорово, правда?

Примерно такая же ситуация и с признаками подобия прямоугольных треугольников.

Признаки подобия прямоугольных треугольников

I. По острому углу

II. По двум катетам

III. По катету и гипотенузе

Медиана в прямоугольном треугольнике

Почему это так?

Рассмотрим вместо прямоугольного треугольника целый прямоугольник.

Проведём диагональ и рассмотрим точку - точку пересечения диагоналей. Что известно про диагонали прямоугольника?

И что из этого следует?

Вот и получилось, что

1. - медиана:

Запомни этот факт! Очень помогает!

А что ещё более удивительно, так это то, что верно и обратное утверждение.

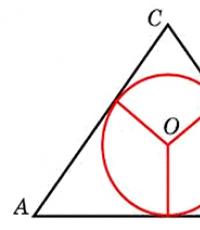
Что же хорошего можно получить из того, что медиана, проведенная к гипотенузе, равна половине гипотенузы? А давай посмотрим на картинку

Посмотри внимательно. У нас есть: , то есть расстояния от точки до всех трёх вершин треугольника оказались равны. Но в треугольнике есть всего одна точка, расстояния от которой о всех трёх вершин треугольника равны, и это - ЦЕНТР ОПИСАННОЙ ОКРУЖНОСТИ. Значит, что получилось?

Вот давай мы начнём с этого «кроме того...».

Посмотрим на и.

Но у подобных треугольников все углы равны!

То же самое можно сказать и про и

А теперь нарисуем это вместе:

Какую же пользу можно извлечь из этого «тройственного» подобия.

Ну, например - две формулы для высоты прямоугольного треугольника.

Запишем отношения соответствующих сторон:

Для нахождения высоты решаем пропорцию и получаем первую формулу "Высота в прямоугольном треугольнике" :

Итак, применим подобие: .

Что теперь получится?

Опять решаем пропорцию и получаем вторую формулу :

Обе эти формулы нужно очень хорошо помнить и применять ту, которую удобнее. Запишем их ещё раз

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: .

Признаки равенства прямоугольных треугольников:

• по двум катетам:
• по катету и гипотенузе: или
• по катету и прилежащему острому углу: или
• по катету и противолежащему острому углу: или
• по гипотенузе и остром углу: или.

Признаки подобия прямоугольных треугольников:

• одному острому углу: или
• из пропорциональности двух катетов:
• из пропорциональности катета и гипотенузы: или.

Синус, косинус, тангенс, котангенс в прямоугольном треугольнике

• Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
• Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
• Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
• Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему: .

Высота прямоугольного треугольника: или.

В прямоугольном треугольнике медиана , проведённая из вершины прямого угла, равна половине гипотенузы: .

Площадь прямоугольного треугольника:

• через катеты:

Анимационное доказательство теоремы Пифагора – одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Считается, что она доказана греческим математиком Пифагором, в честь которого она названа (есть и другие версии, в частности альтернативное мнение, что эта теорема в общем виде была сформулирована математиком-пифагорейцем Гиппасом).
Теорема гласит:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.

Обозначив длину гипотенузы треугольника c, а длины катетов как a и b, получим следующую формулу:

Таким образом, теорема Пифагора устанавливает соотношение, которое позволяет определить сторону прямоугольного треугольника, зная длины двух других. Теорема Пифагора является частным случаем теоремы косинусов, которая определяет соотношение между сторонами произвольного треугольника.
Также доказано обратное утверждение (называют также обратной теореме Пифагора):

Для любых трех положительных чисел a, b и c, таких что a ? + b ? = c ?, существует прямоугольный треугольник с катетами a и b и гипотенузой c.

Визуальное доказательство для треугольника (3, 4, 5) из книги «Чу Пэй» 500-200 до н.э. Историю теоремы можно разделить на четыре части: знание о Пифагоровы числа, знания об отношении сторон в прямоугольном треугольнике, знание об отношении смежных углов и доказательство теоремы.
Мегалитические сооружения около 2500 до н.э. в Египте и Северной Европе, содержат прямоугольные треугольники со сторонами из целых чисел. Бартель Леендерт ван дер Варден высказал гипотезу, что в те времена Пифагоровы числа были найдены алгебраически.
Написанный между 2000 и 1876 до н.э. папирус времен Среднего Египетского царства Berlin 6619 содержит задачу решением которой являются числа Пифагора.
Во время правления Хаммурапи Великого, вивилонська табличка Plimpton 322, написанная между 1790 и 1750 до н.э содержит много записей тесно связанных с числами Пифагора.
В сутрах Будхаяны, которые датируются по разным версиям восьмой или второй веками до н.э. в Индии, содержит Пифагоровы числа выведены алгебраически, формулировка теоремы Пифагора и геометрическое доказательство для ривнобедренного прямоугольного треугольника.
В сутрах Апастамба (около 600 до н.э.) содержится числовое доказательство теоремы Пифагора с использованием вычисления площади. Ван дер Варден считает, что оно было основано на традициях предшественников. Согласно Альбертом Бурко, это оригинальное доказательство теоремы и он предполагает, что Пифагор посетил Араконам и скопировал его.
Пифагор, годы жизни которого обычно указывают 569 – 475 до н.э. использует алгебраические методы расчета пифагоровых чисел, согласно Проклова комментариями к Евклида. Прокл, однако, жил между 410 и 485 годами н.э. Согласно Томасом Гизом, нет никаких указаний на авторство теоремы течение пяти веков после Пифагора. Однако, когда такие авторы как Плутарх или Цицерон приписывают теорему Пифагору, они делают это так, будто авторство широко известно и несомненно.
Около 400 до н. э соответствии Прокла, Платон дал метод расчета пифагоровых чисел, сочетавший алгебру и геометрию. Около 300 до н.э., в Началах Евклида имеем древнейшее аксиоматическое доказательство, которое сохранилось до наших дней.
Написанные где-то между 500 до н.э. и 200 до н.э., китайский математическая книга «Чу Пэй» (? ? ? ?), дает визуальное доказательство теоремы Пифагора, которая в Китае называется теорема гугу (????), для треугольника со сторонами (3, 4, 5). Во время правления династии Хань, с 202 до н.э. до 220 н.э. Пифагоровы числа появляются в книге «Девять разделов математического искусства» вместе с упоминанием о прямоугольные треугольники.
Впервые зафиксировано использование теоремы в Китае, где она известна как теорема гугу (????) и в Индии, где она известна как теорема Баскара.
Многие дискутируется была теорема Пифагора открыта один раз или многократно. Бойер (1991) считает, что знания обнаружены в Шульба Сутра могут быть месопотамского происхождения.
Алгебраическое доказательство
Квадраты образуются из четырех прямоугольных треугольников. Известно более ста доказательств теоремы Пифагора. Здесь представлены доказательства основан на теореме существования площади фигуры:

Разместим четыре одинаковые прямоугольные треугольники так, как это изображено на рисунке.
Четырехугольник со сторонами c является квадратом, так как сумма двух острых углов , А развернутый угол – .
Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной «a + b», а с другой – сумме площадей четырех треугольников и внутреннего квадрата.

Что и необходимо доказать.
По сходству треугольников
Использование подобных треугольников. Пусть ABC – прямоугольный треугольник, в котором угол C прямой, как показано на рисунке. Проведем высоту с точки C, и назовем H точку пересечения со стороной AB. Образован треугольник ACH подобен треугольника ABC, поскольку они оба прямоугольные (по определению высоты), и у них общий угол A, очевидно третий угол будет в этих треугольников также одинаков. Аналогично миркуюючы, треугольник CBH также подобен треугольника ABC. С подобия треугольников: Если

Это можно записать в виде

Если добавить эти две равенства, получим

HB + c times AH = c times (HB + AH) = c ^ 2, ! Src = "http://upload.wikimedia.org/math/7/0/9/70922f59b11b561621c245e11be0b61b.png" />

Другими словами, теорема Пифагора:

Доказательство Евклида
Доказательство Евклида в евклидовых «Началах», теорема Пифагора доказана методом параллелограммов. Пусть A, B, C вершины прямоугольного треугольника, с прямым углом A. Опустим перпендикуляр из точки A на сторону противоположную гипотенузы в квадрате построенном на гипотенузе. Линия делит квадрат на два прямоугольника, каждый из которых имеет такую же площадь, что и квадраты построены на катетах. Главная идея при доказательстве состоит в том, что верхние квадраты превращаются в параллелограммы такой же площади, а потом возвращаются и превращаются в прямоугольники в нижнем квадрате и снова при неизменной площади.

Проведем отрезки CF и AD, получим треугольники BCF и BDA.
Углы CAB и BAG – прямые; соответственно точки C, A и G – коллинеарны. Так же B, A и H.
Углы CBD и FBA – оба прямые, тогда угол ABD равен углу FBC, поскольку оба являются суммой прямого угла и угла ABC.
Треугольник ABD и FBC уровне по двум сторонам и углу между ними.
Поскольку точки A, K и L – коллинеарны, площадь прямоугольника BDLK равна двум площадям треугольника ABD (BDLK = BAGF = AB 2)
Аналогично миркуюючы получим CKLE = ACIH = AC 2
С одной стороны площадь CBDE равна сумме площадей прямоугольников BDLK и CKLE, а с другой стороны площадь квадрата BC 2, или AB 2 + AC 2 = BC 2.

Используя дифференциалы
Использование дифференциалов. Теореме Пифагора можно прийти, если изучать как прирост стороны влияет на ведичину гипотенузы как показано на рисунке справа и применить небольшое вычисления.
В результате прироста стороны a, из подобных треугольников для бесконечно малых приращений

Интегрируя получим

Если a = 0 тогда c = b, так что "константа" – b 2. Тогда

Как можно увидеть, квадраты получен благодаря пропорции между приращениями и сторонами, тогда как сумма является результатом независимого вклада приростов сторон, не очевидно из геометрических доказательств. В этих уравнениях da и dc – соответственно бесконечно малые приращения сторон a и c. Но вместо них мы используем? a и? c, тогда предел отношения, если они стремятся к нулю равна da / dc, производная, и также равен c / a, отношению длин сторон треугольников, в результате получаем дифференциальное уравнение.
В случае ортогональной системы векторов имеет место равенство, которую также называют теоремой Пифагора:

Если – Это проекции вектора на координатные оси, то эта формула совпадает с расстоянием Евклида и означает, что длина вектора равна корню квадратному суммы квадратов его компонентов.
Аналог этого равенства в случае бесконечной системы векторов называется равенства Парсеваля.

Фитнес клуб F3 предлагает выгодные условия на корпоративные фитнес программы для сотрудников Вашей компании.

Итак, какую пользу может принести корпоративный фитнес Вашему бизнесу?

Мотивация сотрудников

Забота о сотрудниках является одной из главных составляющих положительной репутации успешных компаний, а потому корпоративный фитнес – очень важная часть программы повышения их мотивации. Как показала практика, занятия корпоративным фитнесом заметно повышают работоспособность и лояльность сотрудников, существенно снижая показатели больничных пропусков. Кроме того, уютная и непринужденная атмосфера нашего фитнес центра отлично сплочает людей и может послужить целям успешного тим-билдинга. Занятия фитнесом ранним утром заряжают энергией и поднимают настроение на весь день, способствуя мотивации к отдаче и уверенности в себе, а посещение фитнес клуба после работы здорово помогает расслабиться, разгрузить мысли и избавиться от стресса. Ваши сотрудники будут здоровыми, целеустремленными и еще больше полюбят свою работу.

Выгодные условия корпоративного предложения в клубе F 3

Для наших корпоративных клиентов мы предусмотрели наилучшие условия для занятий фитнесом. Приобретая корпоративные карты на 1, 3, 6 или 12 месяцев, Вы получаете скидку в размере …. %. Оплата может производиться как по безналичному, так и наличному рассчету. Условия действуют при заказе корпоративных абонементов для групп от 5 человек и более.

Комплексная корпоративная фитнес программа

Корпоративные фитнес карты предоставляют возможность неограниченного посещения тренажерного зала, кардиозоны и групповых занятий в аэробном зале. Фитнес клуб располагает просторными и чистыми раздевалками – женской и мужской, в каждой из которых предусмотрены надежные шкафчики, туалеты и душевые. Все помещения фитнес клуба F3 совершенно новые и оснащены высококачественной системой вентиляции. Каждая функциональная зона клуба оборудована современными тренажерами и снаряжением премиум-класса от ведущих американских и немецких производителей, занятия с которыми принесут не только неоценимую пользу, но и удовольствие. По-настоящему домашнй уют и дружеская атмосфера F3 помогут стать Вашим сотрудникам дружной и сплоченной командой.

Удобное расположение фитнес клуба

Фитнес клуб F3 находится по адресу Симферопольский проезд, д. 4, в шаговой доступности от Варшаского шоссе, м. Нахимовский проспект и м. Нагорная. Если Ваш офис располагается на юге Москвы, к нам можно легко и быстро добраться на машине и на наземном транспорте от Коломенской, Профсоюзной, Университета, Каширского шоссе и других приближенных точек.

Дополнительные возможности

Корпоративные фитнес программы могут стать еще эффективнее в сочетании с дополнительными бонусами. Ваши сотрудники разрываются между работой и семьей, не имея времени для себя? Для семейных посетителей мы предусмотрели программы Детского фитнеса, которые не только сэкономят время и помогут сплотить семью, но и принесут пользу для здоровья не только родителям, но и детям. Вы также можете заказать услугу Составление персональной программы тренировок или Занятия с персональным фитнес инструктором для одного или двоих, что может стать прекрасным бонусом для поощрения лучших работников или подарком на праздник.

Главная » Советы » Фитнес для корпоративных клиентов. Корпоративным клиентам